Colibri

Structure approximation by a Fourier series

Crystallographic diffraction, like many other physical phenomena, can be expressed through Fourier series.

This animation uses a line drawing of a hummingbird to define a periodic path, the coordinates in the complex plane (x is the real component, y the imaginary one) are a function of time. The path can be approximated by a Fourier series:

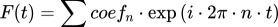
Each coefficient is represented by a rotating arrow, its length is the amplitude and the angle the phase, increasingly higher frequencies can be identified by the speed with which their arrow rotates. Click the links to see the effects of resolution limiting the -otherwise perfect- data as well as for different error levels in the amplitudes or phases as happens in practical crystallography.

The Fourier series approximation is only exact with infinite terms. Increasing the amount of data (high resolution) produces a detailed approximation to the real hummingbird while limiting the data to a few first terms yields low resolution shapes where the hummingbird could not be inferred. Lack of data may lead to the generation of artifacts: it is more intuitive that low resolution data entail a loss of detail (eg. beak) but it should be noted that under such conditions also inexistent features will appear in the image (eg. a rounded tail).

Visualise the effect of errors in the amplitudes (10%, 20%, and 50%) or in the phases (10º, 30º, 45º, 70º, 180º). Errors within the given limit will be randomly generated, giving rise to different distortions depending on the frequencies most affected. In general, larger errors are more deleterious but repeatedly running the same script will show a variety of effects. Errors in phases or moduli of the stronger data -larger arrows more frequent at low frequencies- lead to more noticeable distortion of the image (F-weighted mean phase error is a better measure). Errors in both amplitudes and phases may lead to the generation of artifacts: is your ligand really there even if you see density? As phases are calculated from the current model, local errors cause distortion elsewhere. A wrong model introduces bias and may lead to incorrect structure determination.

(see e.g. 3Blue1Brown video lecture here).